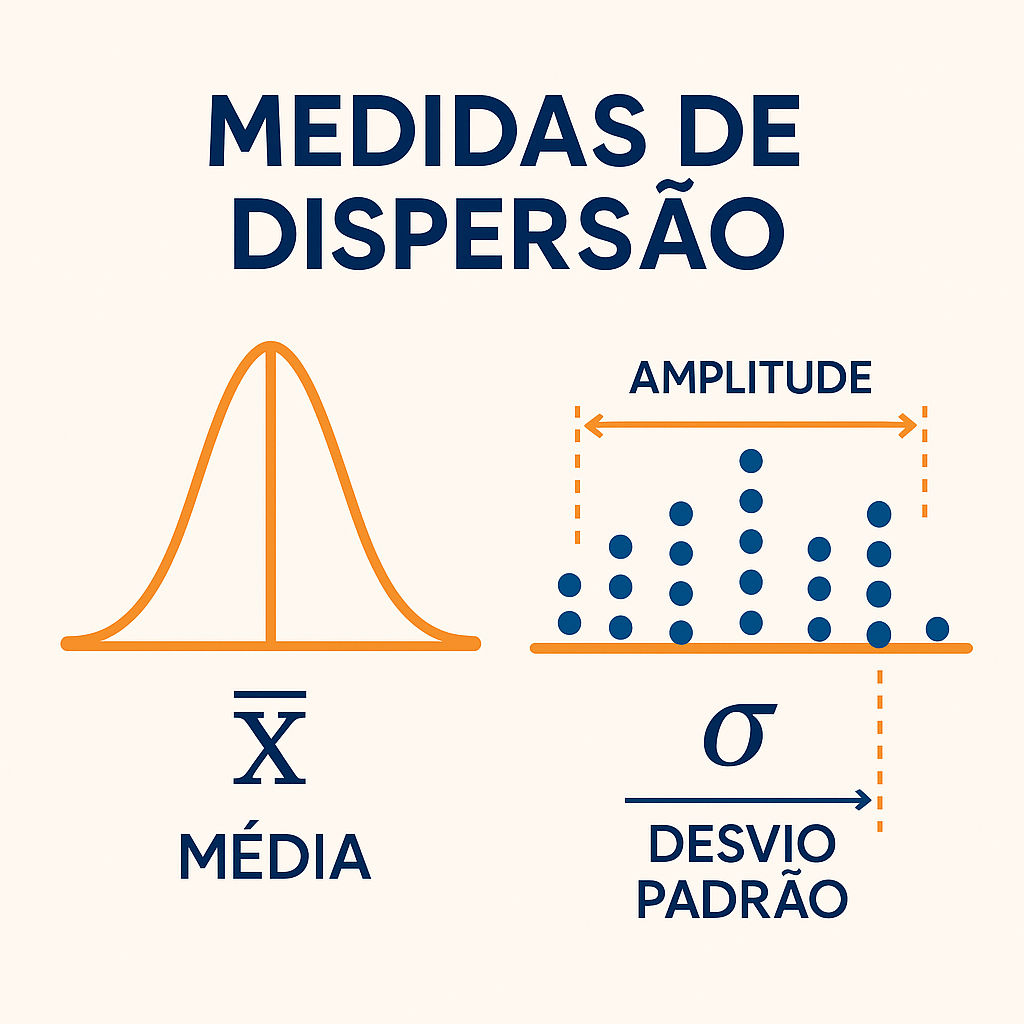
Introdução

Ao trabalhar com dados, muitos analistas focam na tendência central — média, mediana e moda — como resumo da informação. No entanto, tão importante quanto saber onde os dados estão “concentrados” é saber o quão dispersos eles estão. É nesse ponto que as medidas de dispersão se tornam fundamentais.

Como afirma Triola (2015), “medidas de dispersão nos fornecem uma descrição quantitativa da variação dos dados, permitindo distinguir entre conjuntos com a mesma média, mas com comportamentos muito distintos”.

Por que Medidas de Dispersão São Essenciais?

Imagine dois conjuntos de dados com a mesma média. O primeiro tem todos os valores próximos dessa média, enquanto o segundo apresenta valores extremos (outliers). A média, isoladamente, não revela essa diferença. É aí que a dispersão entra: ela mostra o grau de variabilidade dos dados, sua consistência e o risco associado a decisões baseadas nesses dados.

Em contextos como controle de qualidade, finanças, ciências sociais e machine learning, entender essa variabilidade é crítico. Como observa Severino (2013), “as medidas de dispersão não apenas complementam a análise estatística — elas são imprescindíveis para a confiabilidade da interpretação”.

Principais Medidas de Dispersão

1. Amplitude

A amplitude é a diferença entre o maior e o menor valor de um conjunto. É uma medida simples e rápida, mas altamente sensível a outliers. Por exemplo, se a maioria dos valores está entre 10 e 20, mas há um valor 100, a amplitude será exagerada e pouco representativa da maioria.

2. Variância

A variância mede o desvio médio ao quadrado dos dados em relação à média. Ela é útil por considerar todos os valores do conjunto e sua distância da média. A fórmula geral da variância populacional é: σ² = Σ(x - μ)² / N. Para amostras, substituímos N por n – 1.

Embora a variância não esteja na mesma unidade dos dados (por estar ao quadrado), ela serve de base para outras análises, como regressão e testes de hipóteses.

3. Desvio Padrão

O desvio padrão é a raiz quadrada da variância e, por isso, retorna à unidade original dos dados. É a medida de dispersão mais usada. Um desvio padrão alto indica que os dados estão espalhados; um baixo indica concentração em torno da média.

“O desvio padrão tem grande importância prática, sendo amplamente adotado em análises econômicas, financeiras e científicas” (Severino, 2013).

4. Coeficiente de Variação (CV)

O coeficiente de variação é o desvio padrão expresso como porcentagem da média: CV = (σ / μ) × 100. Ele permite comparar a dispersão de dois conjuntos com escalas diferentes. Por exemplo, um CV de 8% indica mais estabilidade do que outro com CV de 35%, mesmo que as médias sejam diferentes.

Aplicações Práticas

Em finanças, o desvio padrão é usado para medir risco de investimento. Em controle de qualidade, a variabilidade dos processos pode indicar falhas operacionais. Em ciência de dados, modelos são mais robustos quando o analista compreende a dispersão das variáveis.

Exemplo: Dois ativos financeiros com a mesma média de retorno (10%). O primeiro tem desvio padrão de 2%, o segundo de 10%. Ambos “rendem” o mesmo, mas o segundo é muito mais arriscado.

Considerações Finais

As medidas de dispersão enriquecem a análise estatística, permitindo decisões mais seguras e conscientes. Elas complementam as medidas de tendência central e são fundamentais em qualquer estudo quantitativo.

Como sintetiza Triola (2015), “a combinação entre média e desvio padrão proporciona um retrato completo da distribuição dos dados”.

Referências

• TRIOLA, Mario F. Introdução à Estatística. 12ª ed. Pearson, 2015.
• SEVERINO, A. J. Estatística Aplicada à Administração. Atlas, 2013.

Publicado em: 20/05/2025 | Por: Decifra Dados