Publicado em: 5 de agosto de 2025

---

Resumo

O teste de hipóteses é um dos pilares fundamentais da inferência estatística, sendo amplamente utilizado em pesquisas científicas, controle de qualidade, avaliações de políticas públicas e estudos de mercado. Este artigo apresenta uma discussão teórica e aplicada sobre os principais conceitos envolvidos no teste de hipóteses, abordando desde a formulação das hipóteses nula e alternativa, até a interpretação do valor-p e dos erros tipo I e tipo II. A partir de referências consolidadas na literatura estatística, destaca-se a importância de uma aplicação consciente e crítica dessa ferramenta no contexto da análise de dados.

1. Introdução

A tomada de decisões baseada em dados é um processo essencial em ambientes científicos, corporativos e governamentais. Nesse contexto, a estatística fornece métodos robustos para lidar com a incerteza e testar proposições sobre populações a partir de informações amostrais. Um desses métodos é o teste de hipóteses, que possibilita avaliar se as evidências empíricas observadas são compatíveis com uma suposição inicial sobre um parâmetro populacional.

Conforme argumentam Montgomery e Runger (2016), os testes de hipóteses constituem uma das aplicações mais importantes da estatística inferencial, pois fornecem um mecanismo formal para verificar se uma suposição sobre um processo ou população pode ser mantida ou rejeitada com base nos dados observados.

2. Fundamentos do Teste de Hipóteses

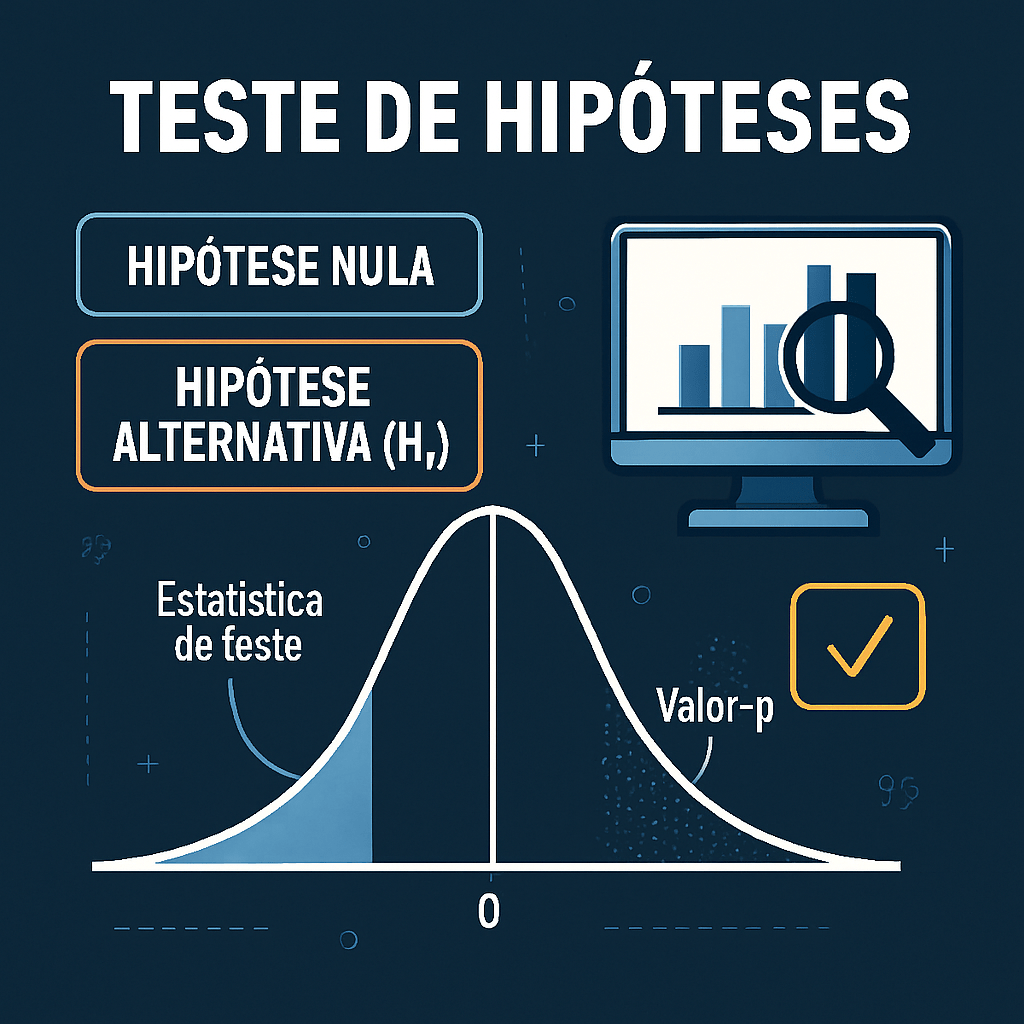
O teste de hipóteses parte da formulação de duas proposições:

• Hipótese nula (H₀): representa o estado atual, assumido como verdadeiro até que se prove o contrário. Costuma refletir a ausência de efeito ou diferença.
• Hipótese alternativa (H₁): representa a afirmação que se deseja testar, geralmente indicando a existência de um efeito, associação ou diferença.

A lógica do teste está ancorada na ideia de falsificação da hipótese nula: ao calcular uma estatística de teste a partir da amostra, verifica-se a probabilidade de obter um resultado tão extremo quanto o observado, caso H₀ seja verdadeira. Essa probabilidade é expressa pelo valor-p.

Segundo Triola (2017), o valor-p quantifica a evidência contra a hipótese nula: quanto menor esse valor, maior a evidência para rejeitá-la. No entanto, o autor destaca que rejeitar H₀ não implica automaticamente a veracidade de H₁, mas apenas indica que os dados são improváveis sob a suposição da hipótese nula.

Moore, McCabe e Craig (2014) afirmam: “O valor-p mede a compatibilidade entre os dados e a hipótese nula. Um valor-p pequeno indica que tal compatibilidade é fraca, sugerindo que a hipótese nula pode não ser verdadeira”.

3. Níveis de significância e erros estatísticos

A tomada de decisão no teste de hipóteses envolve um nível de significância (α), que define a probabilidade máxima tolerável de cometer um erro do tipo I (rejeitar H₀ quando ela é verdadeira). Paralelamente, existe o erro do tipo II (não rejeitar H₀ quando ela é falsa), cuja probabilidade é representada por β.

A relação entre esses erros, o tamanho da amostra e o poder estatístico é crítica para a construção de experimentos robustos. Uma escolha inadequada de α ou um tamanho amostral insuficiente pode comprometer a validade do teste, resultando em conclusões equivocadas com implicações práticas relevantes.

Como ressaltam Wonnacott e Wonnacott (1990): “O uso consciente do teste de hipóteses exige não apenas o conhecimento das regras formais, mas a compreensão das consequências práticas de decisões estatísticas baseadas em probabilidades”.

4. Aplicações práticas do teste de hipóteses

O teste de hipóteses é amplamente utilizado em:

• Pesquisa científica: para testar teorias e validar resultados experimentais;
• Saúde pública: para verificar a eficácia de medicamentos ou intervenções;
• Engenharia e qualidade: para controle estatístico de processos;
• Economia e negócios: para avaliar mudanças em políticas de preços, comportamento do consumidor ou desempenho de produtos;
• Ciências sociais: para comparar grupos e identificar padrões de comportamento.

Montgomery e Runger (2016) observam que, especialmente em ambientes industriais, o teste de hipóteses é fundamental para garantir que processos estejam operando dentro dos padrões esperados, minimizando riscos e otimizando resultados.

5. Considerações finais

O teste de hipóteses é uma ferramenta essencial para a análise estatística e deve ser utilizado com critério e compreensão de suas limitações. A correta formulação das hipóteses, a escolha do nível de significância, a interpretação do valor-p e a consideração dos erros estatísticos são aspectos fundamentais para garantir a validade das conclusões extraídas.

Em suma, o uso adequado do teste de hipóteses não apenas fortalece a análise científica, como também orienta decisões mais embasadas em diversos campos do conhecimento. No entanto, como ressalta Triola (2017), é imprescindível que os analistas estejam atentos aos pressupostos e à natureza probabilística do procedimento, evitando interpretações simplistas ou deterministas dos resultados obtidos.

Referências

• MONTGOMERY, D. C.; RUNGER, G. C. Estatística Aplicada e Probabilidade para Engenheiros. 6. ed. Rio de Janeiro: LTC, 2016.
• TRIOLA, M. F. Introdução à Estatística. 12. ed. São Paulo: Pearson Education do Brasil, 2017.
• MOORE, D. S.; MCCABE, G. P.; CRAIG, B. A. Introduction to the Practice of Statistics. 8th ed. New York: W. H. Freeman, 2014.
• WONNACOTT, T. H.; WONNACOTT, R. J. Estatística: Econometria Básica com Aplicações. 5. ed. São Paulo: Atlas, 1990.